Insolubles: Supplementary Document
This is a supplement my original 2005 article "Insolubles" in the Stanford Encyclopedia of Philosophy .
A Proof Concerning Bradwardine's Theory
Here is a proof that on Bradwardine's theory, every proposition signifies that it is true. Let ‘P’ name the proposition replacing ‘p’. Then:
| 1. | p | Assume for conditional proof. |
| 2. | P signifies that q | Assume for conditional proof. |
| 3. | p → q | From 2 and the "Converse Bradwardine Principle": What propositions signify follows from them. |
| 4. | q | From 1, 3, and modus ponens |
| 5. | (P signifies that q) → q | From 2-4, by conditional proof. |
| 6. | P is true. | From 5 and Bradwardine's definition of truth, since 5 is general with respect to propositions replacing ‘q’. |
| 7. | p → P is true | From 1-6, by conditional proof. |
| 8. | P signifies that P is true. | From 7 and "Bradwardine's Principle": Propositions signify whatever follows from them. |
[Return to Stanford Encyclopedia of Philosophy, "Insolubles," note 19]
The "Converse Bradwardine Principle"
Stephen Read (Read 2002, especially pp. 211-12) has challenged the
view that Thomas Bradwardine was implicitly committed to the co called
"Converse Bradwardine Principle" ("CBP," for
short): whatever a proposition signifies follows from it. Using Read's
notation, let
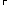 p
p
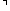 be
a name for the proposition that p (p. 200 n. 12),
and let ‘
be
a name for the proposition that p (p. 200 n. 12),
and let ‘
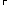 p
p
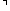 signifies that e’ be symbolized by ‘
signifies that e’ be symbolized by ‘
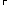 p
p
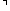 :
e’ (p. 203). Then
:
e’ (p. 203). Then
| CBP | ∀e((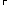 p p
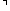 :
e)
→ (p
→ e) :
e)
→ (p
→ e) |
Read and Spade agree that Bradwardine is explicitly committed to the following:
| Definition 1 | The definition of
truth: A true proposition is an utterance signifying only as things
are. T 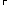 p p
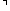 ↔
∀e((
↔
∀e((
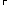 p p
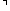 :
e)
→e) :
e)
→e)(Read 2002, p. 191. See Roure 1970, p. 297 § 6.03.) |
| Postulate 2 | The "Bradwardine Principle"
("BP," for short): Whatever follows from a proposition is
signified by it. ∀e((p → e) → 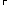 p p
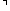 :
e) :
e)(Read 2002, p. 191. See Roure 1970, p. 297 § 6.04.) |
| Postulate 4 | De Morgan's Law. (Read 2002, p. 191. See Roure 1970, p. 297 § 6.04.) |
| Postulate 5 | Disjunctive syllogism. (Read 2002, p. 192. See Roure 1970, p. 297 § 6.04.) |
Read remarks (pp. 211-212):
Spade's reason for attributing CBP to Bradwardine is that "it is presupposed in some of his reasoning" [see Spade 1981, p. 120], in particular, in the second leg of Bradwardine's proof that if A signifies that A is not true and P, then A signifies itself to be true [see Read 2002, pp. 192-93, "Thesis 2"; Spade 1981, pp. 121-23; Roure 1970, p. 299 § 6.054]. But Spade's analysis of the proof … is incorrect … Bradwardine argues as follows: suppose A : (¬TA ∧ P). Since ¬TA → ¬(¬TA ∧ P) by Definition 1 and Thesis 1,[1] ¬TA → (TA ∨ ¬P) by Postulate 4, and so (¬TA ∧ P) → TA by Postulate 5. Hence by Postulate 2, A : TA. Bradwardine does not, and need not use CBP in this proof.
Everything is fine here until the last step, the appeal to Postulate
2 — "Bradwardine's Principle," that propositions
signify whatever follows from them. How could that postulate be
applied here? The first step says that A signifies that
¬TA
∧ P.
The step derived by Postulate 5 states that (¬TA
∧
P)
→
TA. But Postulate 2 cannot be applied to this. The latter
proposition does not say that
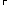 TA
TA
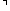 follows from A; it says only that
follows from A; it says only that
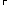 TA
TA
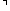 follows from what A signifies. In order to apply Postulate 2
here, we would first have to know that what A signifies
follows from A. But that is just CBP, or at least an instance
of it.
follows from what A signifies. In order to apply Postulate 2
here, we would first have to know that what A signifies
follows from A. But that is just CBP, or at least an instance
of it.
Alternatively, we could assume that A just is
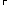 ¬TA
¬TA
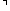 — in effect, that A is the proposition "This very
proposition is not true." In that case, the first step of the
proof is just the hypothesis of the case, and the antecedent of the
second step is just A itself, so that Postulate 2 could
indeed be applied at the end. To be sure, such a case, where
A =
— in effect, that A is the proposition "This very
proposition is not true." In that case, the first step of the
proof is just the hypothesis of the case, and the antecedent of the
second step is just A itself, so that Postulate 2 could
indeed be applied at the end. To be sure, such a case, where
A =
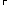 ¬TA
¬TA
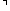 ,
is the most obvious example of what Bradwardine is talking about.
,
is the most obvious example of what Bradwardine is talking about.
But Bradwardine does not restrict himself to this case. His argument
is altogether general; it applies to any proposition that
signifies itself to be not true, no matter what its form. Given the
conventional nature of spoken and written language for medieval
philosophers, the possibilities are endless. For perhaps the simplest
example, let A be the whole conjunction
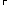 ¬TA
∧ P
¬TA
∧ P
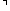 (not just its first conjunct). In that case, the argument above will
not go through as it stands. In short, what Read has shown is not that
Bradwardine's argument does not implicitly appeal to CBP, but only
that a certain more restricted argument does not do so.
(not just its first conjunct). In that case, the argument above will
not go through as it stands. In short, what Read has shown is not that
Bradwardine's argument does not implicitly appeal to CBP, but only
that a certain more restricted argument does not do so.
The confusion between what follows from a proposition and what follows from what it signifies can also be found at Read 2002, p. 195, where he remarks about an argument by Albert of Saxony:
However, there is a suppressed premise, which in full generality would be Bradwardine's crucial Postulate 2 [= "Bradwardine's Principle"], that a proposition signifies whatever is entailed by what it signifies.
But that is not Postulate 2, which states instead that a proposition signifies whatever is entailed by it. The missing link between these two claims is just an instance of CBP.
If I am correct that Bradwardine does implicitly appeal to CBP then, as discussed in n. 19 and shown in the section A Proof Concerning Bradwardine's Theory above, he is likwise committed to the view that all propositions, not just insoluble ones, signify that they are true. Just as Read denies that Bradwardine is committed to CBP, so too he denies that Bradwardine is committed to this latter claim. He says (Read 2002, p. 211):
It is clear that Bradwardine did not accept Buridan's thesis that every proposition implies its own truth. If he had, he would not have given a long and complex proof of the much weaker claim that every insoluble signifies its own truth, or at least, he would have followed it by that stronger claim.
But all this shows is that Bradwardine did not think he was committed to this view. This seems to me to be very likely correct. Nevertheless, if I am right, Bradwardine is committed to it, whether he realized it or not.
Despite our disagreement on these points, Read 2002 contains much valuable information about Buridan's and Albert of Saxony's theories of insolubles and their relations to Bradwardine's theory.
[Return to Stanford Encyclopedia of Philosophy, "Insolubles," note 19]
Note
1. Thesis 1 says (Read 2002, p. 102; see Roure 1970, pp. 297-98 § 6.05):- Every proposition whose terms have many supposita signifies or means affirmation or denial for any of them; and
- if it has only one suppositum, for this or for that.
The correct interpretation of this thesis is not entirely clear, but it is likewise not clear that it is needed at this point in the proof. Bradwardine does not explicitly appeal to it here.